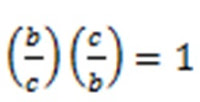RELACIONES TRIGONOMÉTRICAS

DEFINICIÓN DE TRIGONOMETRÍA Y RELACIONES TRIGONOMÉTRICAS

En sus inicios, la trigonometría consistió principalmente en una ciencia del cálculo basada en teoremas geométricos. Los tratados matemáticos de las civilizaciones que precedieron a la Grecia clásica, sobre todo las culturas mesopotámicas, manifiestan algunos cálculos y expresiones que indicaban el desarrollo de una incipiente trigonometría.

Las aportaciones del matemático griego Tales de Mileto (624-548 a.C.), que proporcionaron el surgimiento de las teorías de semejanza o similidad – y que en la actualidad tienen tanta aplicación en el dibujo, los planos, las escalas, la fotografía, entre otras-, son el punto de partida para el desarrollo de la trigonometría.

La palabra trigonometría es un vocablo latino compuesto por trígono, que significa “triángulo” (tres ángulos) y metria “proceso de medir” o “medida”. Esta rama de la geometría tuvo su origen en la necesidad de medir distancias a puntos de difícil acceso, como por ejemplo: la altura de las montañas, el ancho de los ríos, la distancia entre puntos lejanos, etc. Además, la trigonometría permite obtener mayor precisión en algunas medidas, sobre todo cuando la representación gráfica no es exacta.

La trigonometría es la rama de las matemáticas que estudia las relaciones que existen entre los distintos elementos de las figuras geométricas, haciendo énfasis en los ángulos y los lados de los triángulos. Los problemas sobre ángulos y distanciasen un plano corresponden a la trigonometría plana, mientras que los mismos problemas en espacios de dos dimensiones son estudiados por la trigonometría esférica. El estudio de las funciones trigonométricas, que se abordarán a partir de este punto, ha dado origen a la trigonometría analítica.

Los estudios teóricos de la trigonometría se remontan hasta los babilonios, los griegos y los árabes. Sus aplicaciones se daban, principalmente, en la agrimensura, es decir, en la medición de las tierras de cultivo, y en la navegación.

En 1614, el matemático Francés John Napier (1550-1617) descubrió los logaritmos, hecho que favoreció el desarrollo de la trigonometría; no obstante, corresponde a Leonhard Euler, matemático Suizo (1707-1783), la consolidación de esta rama de las matemáticas.

El logaritmo de un número es el exponente al que hay que elevar un número mayor que tomado como base, para obtener el número dado. Si la base es un número a > 1, el logaritmo base a de un número x se representa de la siguiente manera log_ax.

Los logaritmos naturales, cuya base es el número 

, son también conocidos como logaritmos neperianos en honor a John Napier.

En conclusión, se puede plantear que la Trigonometría es el estudio den las relaciones entre los elementos de los triángulos (lados y ángulos). La trigonometría se divide en:

• Trigonometría plana. También es conocida como trigonometría rectilínea porque estudia los triángulos rectilíneos y, en general, los triángulos construidos en los planos.
• Trigonometría del espacio esfera. Su objetivo del estudio son los triángulos esféricos; esto es la región de la superficie de una esfera limitada por los arcos de tres circunferencias máximas.

En este blog solamente estudiaremos la trigonometría plana para la resolución de problemas relativos a los

elementos de triángulos rectángulos y oblicuángulos.


Un ángulo es la amplitud de rotación 

de una semirrecta que gira en sentido contrario a las manecillas del reloj. El lado donde empieza se llama inicial, mientras que el lado al que llega recibe el nombre de terminal o final.

En geometría, solo se considera el ángulo con un valor máximo de una vuelta; es decir, 360° o "pi". En cambio, en trigonometría, la semirrecta puede dar más de una vuelta.

El ángulo se considera positivo, si el giro es en sentido contrario al de las manecillas del reloj, como se observa a continuación:

Mientras que recibe el nombre de ángulo negativo si el giro es en el mismo sentido en el que giran las manecillas del reloj, como a continuación:

Se llama ángulo de elevación si se mide hacia arriba y ángulo de depresión si se mide hacia abajo. Observa que en el ejemplo los dos ángulos son positivos.

RELACIONES TRIGONOMÉTRICAS

Como ya se ha mencionado, la trigonometría se fundamenta en las relaciones entre los lados y los ángulos de un triángulo.

Si trazamos el triángulo OMP en un círculo de radio 10, tendremos los siguientes valore para los lados:

• OP=10
• OM=8
• PM=6
• OP´=10
• OM´=6
• P´M´=8

Si comparamos los lados, tendremos las siguientes razones:

Si el ángulo central aumenta la amplitud de la rotación para formar el triángulo OM´P´ , tendremos las siguientes razones:

Si el ángulo sigue aumentando, la razón variará, por lo que podemos concluir que el valor de la razón depende o está en función del valor o de la amplitud del ángulo. Ese es el motivo por el cual con éstas relaciones o razones trigonométricas podemos definir las funciones trigonométricas.

FUNCIONES TRIGONOMÉTRICAS DEL ÁNGULO AGUDO DE UN TRIÁNGULO RECTÁNGULO

Podemos comparar los lados de un triángulo en función de un ángulo agudo de seis maneras diferentes: las funciones seno, coseno, tangente, cotangente, secante y cosecante. Considera el  

tendremos para el ángulo R.

Los catetos son los lados que forman el ángulo recto.

La hipotenusa es el lado mayor y se opone al ángulo recto.

Según el triángulo de que se trate, los catetos se llaman opuesto o adyacente.

FUNCIONES TRIGONOMÉTRICAS RECÍPROCAS

Dos cantidades recíprocas son aquellas cuyo producto es igual a 1.

 son funciones recíprocas porque 

 

De  lo anterior podemos decir que sen b X csc b  = 1; al despejar tendremos:

son funciones recíprocas porque

De  lo anterior podemos decir que cos b X sec b  = 1; al despejar tendremos:

 son funciones recíprocas porque

 De  lo anterior podemos decir que tan b X cot b  = 1; al despejar tendremos:

FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES: 30° y 60°

Si ABC es un triángulo equilátero de dos unidades por lado, cada uno de sus ángulos mide 60° y la altura divide el ángulo B por la unidad, esto es, 30° cada uno.

Con el teorema de Pitágoras podremos calcular el valor de x en el  

 que es la altura de

FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES: 45 GRADOS

Si construimos un cuadrado ABCD de lado igual a 1 y le trazamos una diagonal, tal como se aprecia en la figura de abajo, tendremos el triángulo isósceles ABC.

Como el triángulo es isósceles, tendrá dos lados iguales y por lo tanto dos ángulos iguales, que son los dos ángulos agudos (a lados iguales se oponen ángulos iguales).

Como sabemos, los ángulos agudos de un triángulo rectángulo suman 90°, lo que significa que cada uno mide 45°.

FUNCIONES TRIGONOMÉTRICAS

FUNCIÓN SENO

El seno de un ángulo es la razón que se establece como cociente del cateto opuesto a la hipotenusa, se abrevia sen; por ejemplo: sen A, quiere decir seno del ángulo A. Si hacemos variar A, a cada uno de sus valores le corresponde un valor de seno. Tenemos así la función sen x, que a cada ángulo x le asocia su seno.

FUNCIÓN COSENO

El coseno de un ángulo es la razón que se establece como cociente del cateto adyacente entre la hipotenusa. Se abrevia Cos. Por ejemplo: Cos A, se lee coseno del ángulo A. Si hacemos variar A, a cada uno de sus valores le corresponde un valor de coseno. Obtenemos así la función cos x , que a cada ángulo x le asocia su coseno.

FUNCIÓN TANGENTE

La tangente de un ángulo es la razón que se establece como cociente del cateto opuesto entre el cateto adyacente; se representa como tan. Por ejemplo: tan A quiere decir tangente del ángulo A.

SIGNOS ALGEBRAICOS DE LAS FUNCIONES

Los ejes coordenados dividen el plano en cuatro cuadrantes nombrados en sentido contrario a las manecillas del reloj.

Los signos de las funciones, según el cuadrante en el cual queda el lado terminal del ángulo, corresponden a los de las tabulaciones de cada función. Se escriben solamente los que tienen sentido positivo, en los demás casos el signo de la función omitida es negativo.

RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS

Resolver un triángulo rectángulo significa encontrar los elementos desconocidos del triángulo, a partir de los elementos que se tienen.

Para determinar un triángulo no es necesario conocer sus seis elementos: tres lados y tres ángulos; es suficiente con tener tres de ellos, siempre que uno sea un lado.

En el caso de los triángulos rectángulos, dado que tienen un ángulo recto, es suficiente con conocer dos de sus elementos, siempre que uno sea un lado.

IDENTIDADES TRIGONOMÉTRICAS

IDENTIDADES TRIGONOMÉTRICAS

IDENTIDADES TRIGONOMÉTRICAS FUNDAMENTALES

Las identidades trigonométricas son igualdades que se cumplen para cualquier valor del ángulo que aparece en la expresión.

Si tenemos el círculo unitario y en él el ángulo MOP donde P (x, y) es el punto en el que el lado final del ángulo corta la circunferencia, entonces:

• X es el valor de la abscisa.
• Y es el valor de la ordenada.

Como ya sabemos que

tenemos entonces dos relaciones principales y de ellas obtenemos cuatro más

RELACIONES PITAGÓRICAS

En un ángulo de 45° se cumple que:

• RM= seno.
• OM = coseno y RM = OM
• PS = tangente
• OS = secante y cosecante
• TS = cotangente y PS = TS

DEMOSTRACIÓN DE LAS IDENTIDADES TRIGONOMÉTRICAS

Demostrar una identidad trigonométrica consiste en comprobar que la igualdad propuesta es cierta para cualquier valor del ángulo que aparece en ella. Para un alumno que es principiante en esta actividad, es recomendable que todos los términos de la igualdad se expresen en función de senos y cosenos, y trabajar en uno de los miembros.

Para demostrar identidades es necesario: conocer bien las identidades trigonométricas fundamentales; dominar el álgebra, principalmente los productos notables y la factorización; manejar las operaciones con fracciones comunes y sobre todo, mucha práctica.

Las siguientes reglas son muy útiles para demostrar identidades trigonométricas:

• ·         Consigue un formulario completo y confiable.
• ·         Si no encuentras la sustitución adecuada, convierte todo a senos y cosenos.
• ·         Si ves un 1 sumando o restando a una función trigonométrica al cuadrado, es probable que sea una identidad pitagórica.
• ·         El 1 es muy importante, así que si en una identidad trigonométrica se escribieron constantes mayores que uno, divide todo entre la constante para obtener la unidad.
• ·         Siempre que puedas, reacomoda los términos, así tendrás otra visión del problema.
• ·         El álgebra es fundamental. Pueden aparecer productos que desarrollar o expresiones que se pueden factorizar.
• ·         Ten cuidado con los denominadores comunes y fíjate en los recíprocos.
• ·         Practica más álgebra y desarrolla tu intuición.

RELACIONES TRIGONOMÉTRICAS EN TRIÁNGULO OBLICUÁNGULOS

Los triángulos oblicuángulos son aquellos que no presentan ningún ángulo recto, por lo que no es posible resolverlos si aplicamos las funciones trigonométricas.

Sin embargo, los triángulos se pueden dividir en otros y aplicar los conocimientos anteriores para generar otros nuevos.

LEYES DE LOS SENOS Y LOS COSENOS

LEY DE LOS SENOS

Supongamos que se tiene la necesidad de resolver el triángulo ABC. Cómo no tiene ángulo recto no podemos aplicar las funciones conocidas, pero si le trazamos una altura sobre el lado que sirve de base, observaremos que se convierte en dos triángulos rectángulos, ya que la altura es una perpendicular de la base.

Despejando h en los dos casos tenemos:

Aplicando la propiedad transitiva:

Si dividimos ambos lados de la igualdad entre ab

Tomando la altura sobre BC y usando el mismo razonamiento obtendremos

Así obtenemos la igualdad conocida como Ley de senos, y la representamos de la siguiente manera:

LEY DE LOS COSENOS

En algunas ocasiones, la ley de los senos no es suficiente para resolver el problema planteado porque faltan datos. Imaginemos por ejemplo que se conocen los tres lados; así al sustituir en la ley de los senos, tendríamos dos incógnitas: los dos ángulos. Para resolver este tipo de problemas se aplica la Ley de los cosenos.

DEMOSTRACIÓN DE LA LEY DE LOS COSENOS

Si tenemos al triángulo ABC

Para el triángulo ACD

Para el triángulo BCD

Si igualamos las dos expresiones para h, aplicando la propiedad transitiva tendremos:

Como:

Entonces:

Y si sustituimos x por su valor, tendremos:

Ésta es la ley de los cosenos. Si despejamos cos A, nos queda:

De esta manera la ley de los cosenos queda así:

Esta ley nos permitirá resolver problemas como el planteado anteriormente.